The given inequality is:
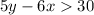
It is required to graph the inequality on a plane.
First graph the boundary line by changing the inequality sign to the equal sign:
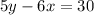
Graph the line using two points.
Find y when x=0:
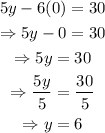
Hence, a point on the boundary line is (0,6).
Find x when y=0:
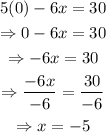
Hence, another point on the boundary line is (-5,0).
Plot the points on the plane and join them with a line :
A broken line is used because the points on the boundary line are not included in the inequality (the sign '>' is used).
Use a test point (0,0) to check the region to shade.
Substitute (x,y)=(0,0) into the inequality and check if it's true:
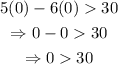
Notice that the inequality is not true.
Hence, plot the test point (0,0) and shade the region that does not contain the test point.
Plot the test point:
Shade the region that does not contain the test point:
The required graph of the inequality is: