Given:
a.) Approximately normal with a mean of 460 and a standard deviation of 31.
b.) The probability that the score of a randomly selected examinee is more than 530.
Step 1: Let's determine the z-score.
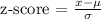
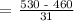
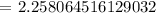
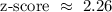
Step 2: Let's use the z-score table to determine its equivalent probability.
From the given chart, it appears that at z-score of 2.26, the probability is 0.9881
Therefore, the answer is 0.9881 or 98.81%