Question

Write the standard form of the equation of the line through the pair of points ( -2, 5 ) and parentheses negative (9, 10 ) Write the equation using only integer coefficients

Answer 1

EXPLANATION

Given the points (x_1,y_1) = (-2,5) and (x_2,y_2) = (9,10), we knows that the slope-intercept form of the linear function is:

y=mx + b where m is the slope and b is the y-intercept

First, we need to find the slope applying the following relationship:

`\text{Slope}=\frac{(y_2-y_1)}{(x_x-x_1_{})}`

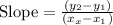
Substituting terms:

`\text{Slope}=((10-5))/(9-(-2))=(5)/(11)`

Now, we need to find the y-intercept:

Considering any point as for instance, (x_1,y_1) = (-2,5) and replacing this in the slope-intercept form:

5=5/11*(-2) + b

Multiplying numbers:

5= -10/11 + b

Adding -10/11 to both sides:

5 + 10/11 = b

Switching sides:

b = 5 + 10/11

Simplifying:

b= 65/11

Then, the slope intercept form of the equation is:

y= 5x/11 + 65/11

Now, multiplying both sides by 11 in order to remove the denominator:

11y = 5x + 65

Subtracting -5x to both sides:

11y -5x = 65

Rearranging terms:

-5x + 11y = 65

So, the Standard Form of the linear equation is:

-5x + 11y = 65