1 Answer

Samir Dangal · Answer 1 · 2023-11-08T14:51:29+0000

We are given the following functions:

$\begin{gathered} q(x)=x^2+6 \\ r(x)=\sqrt[]{x+9} \end{gathered}$

We are asked to determine the following composition of functions:

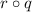
$r\circ q$

This composition is equivalent to the following:

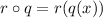
$r\circ q=r(q(x))$

This means that we will substitute the function q(x) for the value of "x" in the function r(x), like this:

$r(q(x))=\sqrt[]{(x^2+6)+9}$

Now, we add like terms:

$r(q(x))=\sqrt[]{x^2+15}$

Now, since we are asked about the composition when x = 7 we will substitute the values of "x = 7" in the resulting function:

$r(q(7))=\sqrt[]{(7)^2+15}$

Now, we solve the operations:

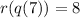
Therefore, the value of the composition of function at "x = 7" is 8. We can use the same procedure to determine the composition of q and r.

Please log in or register to add a comment.