Question

State ALL possible values for x that would satisfy the following inequalities/equation. Graph on a number line a. - 4x + 3 < 11 b. - 4x > 8 c. - 4x = 12

Answer 1

A)

Starting with the inequality:

`-4x+3<11`

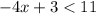
Substract 3 from both sides of the inequality:

`\begin{gathered} -4x<11-3 \\ \Rightarrow-4x<8 \end{gathered}`

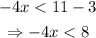
Divide both sides of the inequality by -4. Since -4 is a negative number, swap the < sign:

`\begin{gathered} -(4x)/(-4)>(8)/(-4) \\ \Rightarrow x>-2 \end{gathered}`

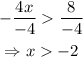
Plot the relation -2 on a number line:

B)

Use similar arguments, be careful of dividing by negative numbers, as that will change the orientation of the symbol "<" or ">".

This time, the final expression is:

`x<-2`

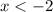
Plot in the number line:

C)

Divide both sides by -4 to get:

`x=-3`

Plot by drawing a single point at x=-3:

Recall the properties of inequalities:

Let a, b and c be real numbers.

If:

`aThen:[tex]\begin{gathered} b>a \\ a+c-b \end{gathered}`

If c is positive, then:

In other words: the orientation of the inequality symbol does not change when adding or substracting quantities, and remains the same when multiplying or dividing by a positive number.

The orientation of the inequality symbol changes when the inequality is multiplied or divided by a negative number. This includes multiplying by -1. When writing the inequality by taking the right side to the left and vice versa, the inequality symbol should also swap.