(a) The random variable in this experiment is the number of aces in the experiment, that is all possible values of x {0,1,2,3}
(b) Given that the number of standard deck of cards is 52 and there are 4 aces, the probability of picking an ace is
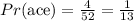
The probability of success and failure in this case is shown below
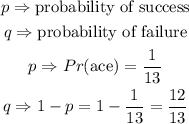
To construct a probability distribution table for the number of aces for x values equal to 0,1,2,3. We are going to use binomial distribution formula, the binomial distribution formula is shown below
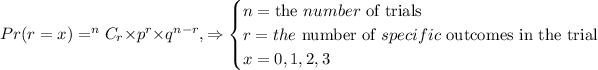
For x=0
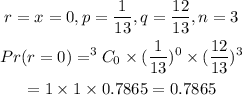
For x=1
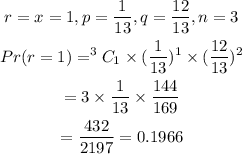
For x=2
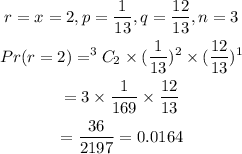
For x=3
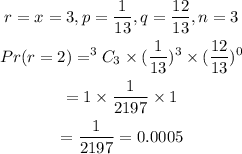
Answer: The probability distribution table is shown below