We will need to use the following formulas
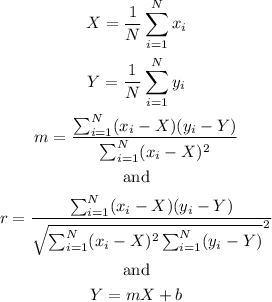
In our case, using a calculator
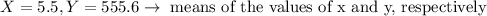
Therefore,
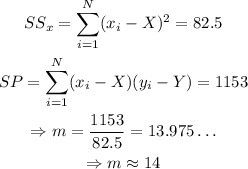
Finding b,
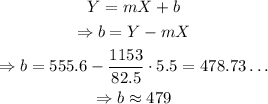
Thus, the equation of the line of best is y=14x+479.
As for the correlation coefficient,
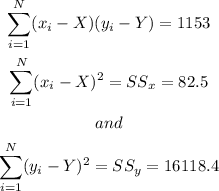
Therefore,
![\begin{gathered} \Rightarrow r=\frac{1153}{\sqrt[]{82.5\cdot16118.4}}=0.9998\ldots\approx1 \\ \Rightarrow r=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q7f3qnc8gyd7wx6pwre38ercvez6f49b8e.png)
Then, the Correlation Coefficient is r=1.
The r is practically 1, the model is considered a good fit; in fact, it is a perfect fit (strong relationship)
Summation Notation
Consider the expression
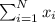
Notice that there are 10 values of x in the table, order them in the following way
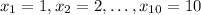
Then, after setting N=10,
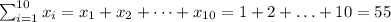
Another example,

We found that X=5.5 (see above); then,
![\begin{gathered} \sum ^(10)_(i=1)(x_i-X)^2=(x_1-X)^2+(x_2-X)^2+\cdots(x_(10)-X)^2=(1-5.5)^2+(2-5.5)^2+\cdots(10-5.5)^2 \\ \Rightarrow\sum ^(10)_(i=1)(x_i-X)^2=(1-5.5)^2+(2-5.5)^2+\cdots(10-5.5)^2 \end{gathered}]()