Question

A busboy uses a 15N force to push a 25kg cart at constant speed. If the waiter is pushing down at a 37 degree angle, find the normal force and friction

Answer 1

`\begin{gathered} N=245N \\ Fr\approx11.98N \end{gathered}`

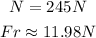
Step-by-step explanation

First, let us make a sketch of the problem:

The normal force has the same magnitude as the weight of the cart.

`N=mg`

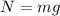
where m = mass; g = acceleration due to gravity

Hence, the normal force is:

`\begin{gathered} N=25\cdot9.8 \\ N=245N \end{gathered}`

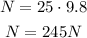
Applying Newton's second law of motion in the horizontal direction, the sum of forces acting on the cart is:

`\sum F_x=ma_x=-Fr+Fp\cos 37_{}`

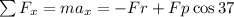
where Fp = force of the push

Fr = friction force

Since the waiter pushes the cart at a constant speed, it means that the acceleration of the cart (ax) is 0.

This implies that:

`0=-Fr+15\cos 37`

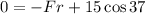
Solve for Fr:

`\begin{gathered} \Rightarrow Fr=15\cos 37 \\ \Rightarrow Fr\approx11.98N \end{gathered}`

That is the friction force.