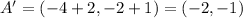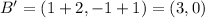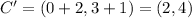Question

Triangle ABC will dilated about the point (2, 1) by a scale factor of .8c7863 21-8-7-8-5-4-3-2-1 0234578- 1-В2А-3-4-5-8Identify the coordinates of the vertices after the transformation.A'BC

Answer 1

We should first recognize that a dilation by a scale factor of 1/2 is actually a compression.

We are told the compression is done about the point (2,1):

What we should do is translate the whole figure so the origin is the point about which we do the compression. To do this, we subtract 2 from the x-coordinate of each vertex and we subtract 1 from the y-coordinate of each vertex.

With this in mind, to coordinates of the translation (TA, TB, TC) will be:

`TA^{^{}}=(-6-2,-3-1)=(-8,-4)`
`TB=(4-2,-1-1)=(2,-2)`

`TC=(2-2,7-1)=(0,6)`

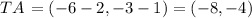
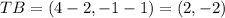
Now we multiply this new coordinates by the scale factor to obtain a new set of coordinates (A'', B'', C''):

`A^(\doubleprime)=(1)/(2)(-8,-4)=(-4,-2)`
`B^(\doubleprime)=(1)/(2)(2,-2)=(1,-1)`
`C^(\doubleprime)=(1)/(2)(1,6)=(0,3)`

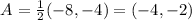
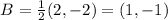
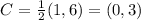
Finally, we translate the figure back were we started, so we add 2 to the x-coordinate and 1 to the y-coordinate to obtain A', B' and C':

`A^(\prime)=(-4+2,-2+1)=(-2,-1)`
`B^(\prime)=(1+2,-1+1)=(3,0)`
`C^(\prime)=(0+2,3+1)=(2,4)`