The following equations represent two families babysitting payment plans.
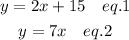
Where y represents the wages earned and x represents the hours worked.
Let us solve this system of equations to find out when do the two plans pay the same and how much do they pay?
Substitute eq.2 into eq.1 and solve for x
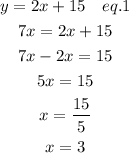
This means that the two plans pay the same when they work for 3 hours.
Substitute x = 3 into eq.2 to find the value of y
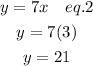
This means that the plan pays $21 when they work for 3 hours.
Therefore, the solution is
x = 3 hours
y = $21