Question

Who is climbing at a faster rate?and how much faster does that person climb per hour?

Answer 1

The altitude and time of both Malik and Mila are provided in function form. The rate of climb can be gotten by evaluating the slope of the functions/graphs.

To calculate the slope, we use the formula:

`m=(y_2-y_1)/(x_2-x_1)`

Mila's Ascension:

We have the following parameters from the table:

`\begin{gathered} (x_1,y_1)=(1,721) \\ (x_2,y_2)=(2,1442) \end{gathered}`

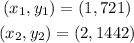
Hence, we can calculate the rate of climb to be:

`\begin{gathered} m_1=(1442-721)/(2-1) \\ m_1=721 \end{gathered}`

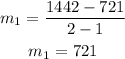
Therefore, Mila ascends at 721 ft/h.

Malik's Ascension:

We have the following parameters from the graph:

`\begin{gathered} (x_1,y_1)=(1,693) \\ (x_2,y_2)=(2,1386) \end{gathered}`

Hence, we can calculate the rate of climb to be:

`\begin{gathered} m_2=(1386-693)/(2-1) \\ m_2=693 \end{gathered}`

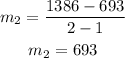
Therefore, Malik ascends at 693 ft/h.

The difference between both ascension rates is how much faster one is going than the other. This is given to be:

`D=m_2-m_1=721-693=28`

ANSWERS:

1) Mila is climbing at a faster rate.

2) Mila is climbing faster than Malik at a rate of 28 ft/h.