We are given the following information
Line AC and EG are perpendicular.
Angle FBC is the complement of the angle ABD.
Angle FBC = (x + 4)°
Angle ABD = (5x - 10)°
We are asked to find the angle EBF.
Recall that when two angles are complementary then they add up to 90°
So we can write
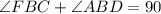
Let us substitute the given values and solve for x.
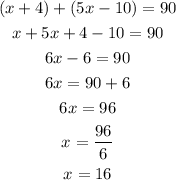
So the angle FBC is
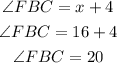
Since we know that lines AC and EG are perpendicular so the angle FBC and angle EBF must add up to 90°
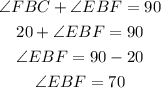
Therefore, the angle EBF is 70°.