Let x be the number of pounds of the first type ($4.40) of nut, and y be the number of pounds of the other one, then we can set the following system of equations:

Solving the first equation for x we get:
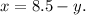
Substituting the above result in the second equation we get:
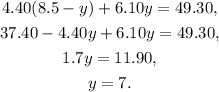
Substituting y=7 in the third equation on the board we get:

Answer: You will need to add 1.5 pounds of the $4.40 nut and 7 pounds of the other one.