Question

Points Scored per Player Team A Team B 6 5 B 9 18 7 110 9 13 13 115 11 14 13 20 15 17 14 4 10 8) Find the mean of scores for Team A and Team B. Which team had the greater mean? 9) Find the variance of Team A. Use the formula for o? (divide by how many). 10) Then find the standard deviation of Team A scores. Use the formula for o (divide by how many).

Answer 1

(a)The mean scores for Team A and B are 7.9 and 10.6 respectively.

(b)Variance for Team A scores =29.49

(c)Standard deviation for Team A scores = 5.43

Explanation:

The points scored per player in each team is:

• Team A: 6,2,8,10,3,15,4,20,7,4

,

• Team B: 5,9,7,9,13,11,13,15,14,10

Part A

We find the mean by adding all the points and dividing by the number of players 10.

`\begin{gathered} \text{Mean Points for Team A} \\ =(6+2+8+10+3+15+4+20+7+4)/(10)=(79)/(10) \\ =7.9 \end{gathered}`

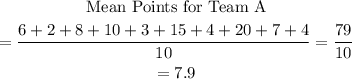
Similarly:

`\begin{gathered} \text{Mean Points for Team B} \\ =(5+9+7+9+13+11+13+15+14+10)/(10)=(106)/(10) \\ =10.6 \end{gathered}`

The mean scores for Team A and B are 7.9 and 10.6 respectively.

Part B (Variance for Team A)

To calculate the variance, we make use of the formula below:

`\sigma^2=(\sum_(i=1)^(n)\left(x_(i)-\mu\right)^(2))/(n)`

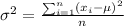
Using the table below:

Therefore:

`\begin{gathered} \text{Variance,}\sigma^2=(\sum^n_(i=1)(x_i-\mu)^2)/(n)=(294.9)/(10) \\ \sigma^2=29.49 \end{gathered}`

The variance of Team A scores is 29.49.

Part C (Standard deviation of Team A scores)

The standard deviation is the square root of the variance.

From part (B), variance = 29.49

Therefore:

`\sigma=\sqrt[]{29.49}=5.43`

The standard deviation of Team A scores is 5.43.