Given:
The word, "METAPHOR".
To find:
The number of three letter arrangements.
Step-by-step explanation:
There are 8 letters.
Therefore, n = 8.
Out of 8 letters, we need to select 3 letters.
So, r = 3.
Using the permutation,
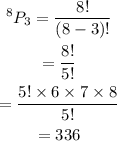
Therefore, the number of three-letter arrangements is 336.
Final answer:
The number of three-letter arrangements is 336.