Given the expression:
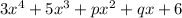
Factors of the expression are:
(x - 2) and (x +3).
Let's find the values of p and q.
To solve for p and q, take the following steps:
Step 1:
Equate the factors to zero and solve for x.
x - 2 = 0
Add 2 to both sides:
x - 2 + 2 = 0 + 2
x = 2
x + 3 = 0
Subtract 3 from both sides:
x+ 3 - 3 = 0 - 3
x = -3
Thus, we have:
x = 2 and -3
Step 2:
Now, solve the expression for f(2) and f(-3).
We have:
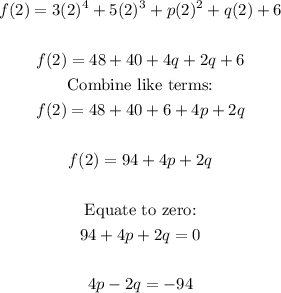
Solve for f(-3):
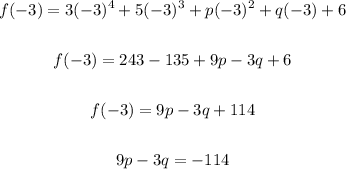
Now, we have the set of equations:
4p - 2q = -94..................equation 1
9p - 3q = - 114..................equation 2
Step 3:
Solve the set of equations simultaneously using the elimination method.
4p - 2q = -94
9p - 3q = -114
Multilply all terms in equation 1 by -3 and equation two by 2:
4p(-3) - 2q(-3) = -94(-3)
9p(2) - 3q(2) = -114(2)
-12p + 6q = 282................equation 3
18p - 6q = -228,...............equation 4
Add both equation 3 and 4
-12p + 6q = 282
+ 18p - 6q = -228
--------------------------------
6p + 0 = 54
6p = 54
Divide both sides by 6:
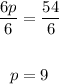
Substitute 9 for p in equation 1:
4p - 2q = -94
4(9) - 2q = -94
36 - 2q = -94
Subtract 36 from both sides:
36 - 36 - 2q = -94 - 36
-2q = -130
Divide both sides by -2:

Therefore, the values of p and q are:
p = 9
q = 65
ANSWER:
p = 9 and q = 65