Number of $10 coins =
Number of $20 coins
STEP - BY - STEP EXPLANATION
What to find?
• Number of $10 coins.
,
• Number of $20 coins.
Given:
• Total number of coins = 43
,
• Total value of coins = $660
To solve the given problem, we will follow the steps below:
Step 1
Translate the given problem into an equation.
Let x be number of $10 coins.
Let y be number of $20 coins.
x + y = 43 -----------------------------------(1)
10x + 20y = 660 ----------------------------------(2)
Step 2
Using substitution method to solve, make x the subject of formula in equation (1).
x= 43 - y
Step 3
Substitute the result in step 2 into equation (2).
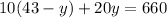
Step 4
Open the prenthesis.
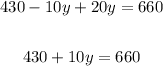
Step 5
Subtract 430 from both-side of the equation.
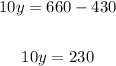
Step 6
Divide both-side of the equation by 10.
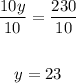
Step 7
Substitute the value of y into x=43 - y and solve for x.
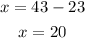
Therefore, he has 20 numbers of $10 and 23 numbers of $20.