Question

An object of mass 2.5 kg sliding on a horizontal frictionless surface with a speed of 4m / s collides with a horizontal relaxed spring as shown in the figure . If the spring is compressed by a distance of 40 cm and the block comes to rest , then the spring constant k is equal to :

Answer 1

Given:

The mass of the object is,

`m=2.5\text{ kg}`

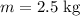
The speed of the object is,

`v=4\text{ m/s}`

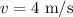
The compression of the spring is,

`\begin{gathered} x=40\text{ cm} \\ =0.40\text{ m} \end{gathered}`

To find:

The spring constant

Step-by-step explanation:

The kinetic energy of the box provides the potential energy of the spring.

If the spring constant of the spring be 'k', the potential energy is,

`(1)/(2)kx^2`

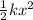
The kinetic energy of the mass is,

`(1)/(2)mv^2`

Now we can write,

`\begin{gathered} (1)/(2)kx^2=(1)/(2)mv^2 \\ k=m(v^2)/(x^2) \end{gathered}`

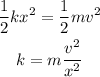
Substituting the values we get,

`\begin{gathered} k=2.5*(4*4)/(0.40*0.40) \\ =250\text{ N/m} \end{gathered}`

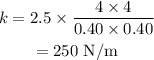
Hence, the spring constant is 250 N/m.