Question

Find the equation of the line passing through (5,2) and (-1,4). Write your answer in general form.

Answer 1

Recall that the general form of a straight line is

`Ax+By+C=0`

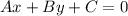
where A,B and C are real numbers.

To find this equation, we will first find the slope intercept form of the line and then apply mathematical operations so we get the form we are looking form. Recall that the slope-intercept form of a line is of the form

`y=mx+b`

where m is the slope and b is the y intercept. We will first find the slope.

Recall that the slope of a line that passes through the points (a,b) and (c,d) is given by the formula

`m=\frac{d\text{ -b}}{c\text{ -a}}=\frac{b\text{ -d}}{a\text{ -c}}`

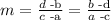
so in our case we have a=5,b=2, c=-1 and d=4. So we get

`m=\frac{4\text{ -2}}{\text{ -1 -5}}=\frac{4\text{ -2}}{\text{ -1 -5}}=\text{ -}(2)/(6)=\text{ -}(1)/(3)`

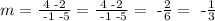
So far, our line equation would look like this

`y=\text{ -}(1)/(3)x+b`

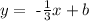
Note that as we want this line to pass through the point (5,2), this means that if we replace x=5 in this expression we should get y=2. So we have

`2=\text{ -}(1)/(3)\cdot5+b`

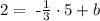
so if we add 5/3 on both sides, we get

`b=2+(5)/(3)=(11)/(3)`

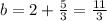
so our equation becomes

`y=\text{ -}(1)/(3)x+(11)/(3)`

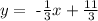
Now, from this equation we can look for the general form. First, we will multiply both sides by 3, so we get

`3y=\text{ -x+11}`

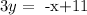
now, we add x on both sides, so we get

`x+3y=11`

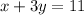
Finally, we subtract 11 on both sides, so we get

`x+3y\text{ -11=0}`

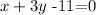
which is the general form of the line