Given:
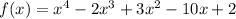
Requirement:
To check whether (x-2) is a factor of a given equation or not using remainder method.
Step-by-step explanation:
By putting x = 2 in the given equation we get
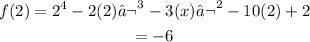
Since f(2) = -6 it meant it will give -6 as a remainder after dividing the equation by (x - 2)
Hence, (x - 2) is not a factor of the given equation.
Final Answer:
(x - 2) is not a factor of the given equation.