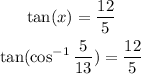In the right triangle, there are 2 legs of the right angle and one hypotenuse (the side opposite to the right angle
The ratio cos(x) = adjacent side to the angle x/ hypotenuse
Then if cos(x) = 5/13, then
That means the adjacent side to angle x = 5 and the hypotenuse = 13
Let us draw the sketch
To find tan we have to find the other leg of the right angle which is opposite to angle x
We will use the Pythagoras Theorem
![\begin{gathered} L=\sqrt[]{13^2-5^2} \\ L=\sqrt[]{169-25} \\ L=\sqrt[]{144} \\ L=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a6frhxkuuj5lb4swpvlywa1o9v87t0g9as.png)
Since tan(x) = opposite side to x/ adjacent side to x
Since the opposite side is 12
Since the adjacent side is 5, then