Question

Short step please.I did #16 but now I dont Know how to do #17

Answer 1

From the values above we have the mean to be

`\mu_x=1.4`

Step 1:

We will figure out the values of

`x-\mu_x`
`\begin{gathered} x-\mu_x=0-1.4=-1.4 \\ x-\mu_x=1-1.4=-0.4 \\ x-\mu_x=2-1.4=0.6 \\ x-\mu_x=3-1.4=1.6 \end{gathered}`

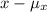
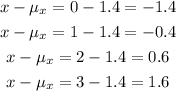
Step 2:

We will figure out the values of

`(x-\mu_x)^2`
`\begin{gathered} (x-\mu_x)^2=(-1.4)^2=1.96 \\ (x-\mu_x)^2=(-0.4)^2=0.16 \\ (x-\mu_x)^2=(0.6)^2=0.36 \\ (x-\mu_x)^2=(1.6)^2=2.56 \end{gathered}`

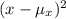
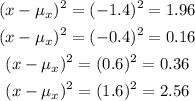
Step 3:

We will figure out the value of

`(x-\mu_x)^2.P(x)`
`\begin{gathered} (x-\mu_x)^2.P(x)=0.1*1.96=0.196 \\ (x-\mu_x)^2.P(x)=0.6*0.16=0.096 \\ (x-\mu_x)^2.P(x)=0.36*0.1=0.036 \\ (x-\mu_x)^2.P(x)=2.56*0.2=0.512 \end{gathered}`

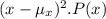
Step 4:

We will calculate the variance of the distribution using the formula below

`\begin{gathered} \sum_{n\mathop{=}0}^(\infty)(x-\mu_x)^2.P(x)=0.196+0.096+0.036+0.512 \\ variance=0.84 \end{gathered}`

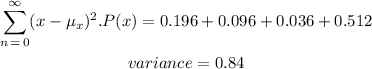
Hence,

The variance is = 0.84

Step 5:

To calculate the standard deviation, we will use the formula below

`\begin{gathered} \sigma=√(variance) \\ \sigma=√(0.84) \\ \sigma=0.917 \end{gathered}`

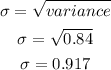
Hence,

The standard deviation is = 0.917