To find all those values, first, let's order our dataset from smallest to largest number.
We have the following set:
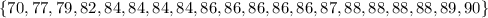
The median for an even set of numbers is the mean between the two elements "in the middle" of the set. This set has 20 elements, which means our median is the mean between the 10th and the 11th elements(they are in the middle because they have 9 elements below them, and 9 elements above).
Those elements are 86 and 86. Since they are the same number, our median is 86.
Now, let's calculate the mean value. The mean value is just the sum of all elements divided by the total amount of elements.

In this case, our 'n' is 20. Doing the calculation, we have:
![\begin{gathered} \bar{x}=(1)/(20)(70+90+88+89+86+86+86+86+84+82+77+79+86+84+84+84+87+88+88+88) \\ =84.6 \end{gathered}]()
Then, we have our mean. The mean is 84.6.
The mean absolute deviation, is given by the following formula:
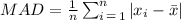
Since we already calculated the mean previously, our MAD will be
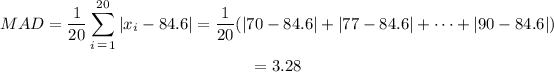
MAD is equal to 3.28.
To find the interquartile range, we're going to divide our ordered set into two sets, "cutting" it in the middle.

Now, let's find the median for each one of those sets. Using the same process we did before, the medians are 84 and 88 respectively. The interquartile range is given by the difference between those medians.
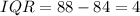
Our interquartile range is equal to 4.