Question

Let f(x)=4x+8 and g(x)=5x^2. Perform the function operation and then find the domain of the result. (f+g)(x)

Answer 1

The sum of functions is defined like this:

`(f+g)(x)=f(x)+g(x)`

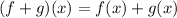
In this case, we have:

`\begin{gathered} f(x)=4x+8 \\ g(x)=5x^2 \\ (f+g)(x)=f(x)+g(x) \\ (f+g)(x)=4x+8+5x^2 \\ \text{ Reorder} \\ (f+g)(x)=5x^2+4x+8 \end{gathered}`

The found function is quadratic because the degree of the polynomial is 2. The degree of a polynomial is the highest exponent vale of ant of its terms.

The domain of any quadratic function is all real values.

Thus, the domain of the sum of the given functions is:

`$$\boldsymbol{D=(-\infty,\infty)}$$`