Question

A chemist has 20% and 50% solutions of acid available. How many liters of each solution should bemixed to obtain 93.75 liters of 28% acid solution?liters of 20% acidliters of 50% acid

Answer 1

Given the word problem, we can deduce the following information:

1. A chemist has 20% and 50% solutions of acid.

2. The solution should be mixed to obtain 93.75 liters of 28% acid solution.

To determine the amount of liters of each solution, the equation we should use is:

`\begin{gathered} 0.2x+0.5(93.75-x)=0.28(93.75) \\ \end{gathered}`

where:

x= amount of liters

We simplify the equation and rearrange to get the value of x:

`\begin{gathered} 0.2x+0.5(93.75-x)=0.28(93.75) \\ 0.2x+46.875-0.5x=26.25 \\ -0.3x+46.875=26.25 \\ -0.3x=26.25-46.875 \\ -0.3x=-20.625 \\ x=-(20.625)/(-0.3) \\ x=68.75\text{ Liters} \end{gathered}`

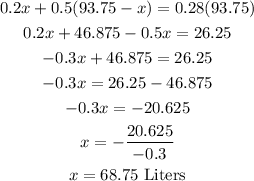
For 20% acid, the amount in liters is 68.75. While to get for 50% acid is by:

93.75-68.75 = 25 Liters

Therefore, the answer is:

68.75 liters for 20% acid

25 liters for 50% acid.