Question

If y varies directly as x and y=80 when x=32 find x when y = 100.

Answer 1

Answer: x=40 and y=100!
Hope this helped

Answer 2

Since y varies directly as x, we have that this expression is true:

`y=kx`

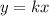
Now, we are given the information that y=80 when x=32, then we can find k easily like this:

`\begin{gathered} y=kx \\ \Rightarrow80=k\cdot(32) \\ \Rightarrow k=(80)/(32)=(5)/(2) \\ k=(5)/(2) \end{gathered}`

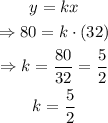
Finally, to find x when y=100, we substitute each value and solve for x the resulting expression:

`\begin{gathered} y=kx \\ \Rightarrow100=(5)/(2)\cdot x \\ \Rightarrow100\cdot2=5x \\ \Rightarrow200=5x \\ \Rightarrow x=(200)/(5)=40 \\ x=40 \end{gathered}`

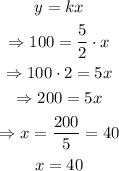
Therefore, x=40 when y=100