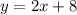Question

Find an equation for the perpendicular bisector of the line segment whose endpoints(3, -1) and (-9,5).are

Answer 1

To find the equation you need to find the slope:

1. Find the midpoint coordinates:

`\begin{gathered} \text{midpoint}=((x_1+x_2)/(2),(y_2+y_1)/(2)) \\ \\ \text{midpoint}=((3-9)/(2),(-1+5)/(2)) \\ \\ \text{midpoint}=(-(6)/(2),(4)/(2)) \\ \\ \text{midpoint}=(-3,2) \end{gathered}`

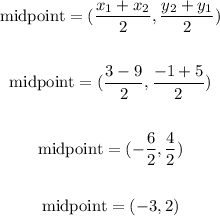
The perpendicular bisector passes throuhg point (-3,2)

2. Find the slope (m) of the line segment:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \\ m=(5-(-1))/(-9-3)=(5+1)/(-12)=-(6)/(12)=-(1)/(2) \end{gathered}`

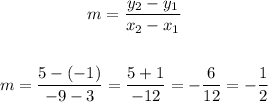
3. Fidn the slope of perpendicular bisector:

Perpendicular lines have negative reciprocal slopes:

The slope of perpendicular bisector is: -1/slope of line segment:

`m=-(1)/(-(1)/(2))=2`

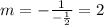
4. Find the y-intercept (b) of the perpendicular bisector:

Use the point (-3,2) and the slope 2

`\begin{gathered} y=mx+b \\ 2=2(-3)+b \\ 2=-6+b \\ 2+6=b \\ 8=b \end{gathered}`

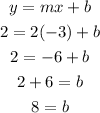
Then, the squation of the perpendicular bisector is:

`y=2x+8`