Given
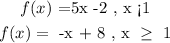
Required: f(-2) + f(3)
The given function f(x) is a piece-wise function . This implies that the function is defined differently at different range of x
For the given problem
At x = -2
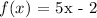
Substituting the value of x into f(x):
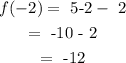
At x = 3
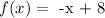
Substituting the value of x into f(x):
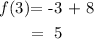
Next, we sum f(-2) and f(3):
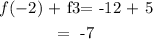
Answer: -7 (Option B)