Question

What percentage of the speed of light will an electron be moving after being accelerated through a potential difference of 1,844 Volts?

Answer 1

Answer:

The electron will be moving at 8.5% of the speed of light

Step-by-step explanation:

The mass of an electron is:

`m=9.1*10^(-31)kg`

The potential difference, V = 1844 Volts

The charge of an electron is:

`e=1.6*10^(-19)`

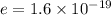
The speed of the electron is calculated below

`\begin{gathered} v=\sqrt{(2eV)/(m)} \\ \\ v=\sqrt{(2*1.6*10^(-19)*1844)/(9.1*10^(-31))} \\ \\ v=25464476.4\text{ m/s} \end{gathered}`

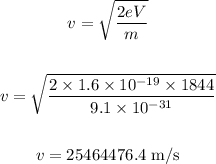
The speed of light is:

`c=8*10^8\text{ m/s}`

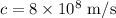
The percentage of the speed of light that the electron will move is:

`\begin{gathered} (25464476.4)/(3*10^8)*100\% \\ \\ =8.5\% \end{gathered}`

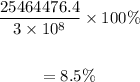
The electron will be moving at 8.5% of the speed of light