Question

Help me with B and C please! The answer to A is 500

Answer 1

B)

F(t) is continuous for a given value of t if, and only if, the limit for F(t) for t approaching this values by the left and by the right result in the same value. To check it, let us to calculate it, as follows:

`\begin{gathered} lim_(t\rightarrow4^-)^\text{ \lparen}5\cdot2^(t+1)-3)=5\cdot2^(4+1)-3= \\ \\ =5\cdot2^5-3=5\cdot32-3=160-3=157 \end{gathered}`
`\begin{gathered} lim_(t\rightarrow4^(^+))((500t-1500)/(t-1))=(500\cdot4-1500)/(4-1)= \\ \\ (2000-1500)/(3)=(500)/(3)\cong166.7 \end{gathered}`

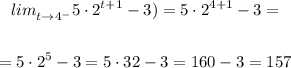
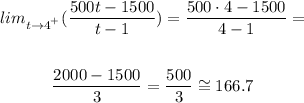
Because the calculation of both side-approaching limits results in different values, we are able to conclude that: The function is not continuous.

C)

To the given equation, we just need to substitute M(t) = 100 and isolate t to find its value, as follows:

`\begin{gathered} M(t)=100=(210(2^t-1))/(2^t+5)\Rightarrow10(2^t+5)=21(2^t-1) \\ \\ \Rightarrow10\cdot2^t+50=21\cdot2^t-20\Rightarrow21\cdot2^t-10\cdot2^t=50+20 \\ \Rightarrow11\cdot2^t=70\Rightarrow2^t=(70)/(11)\Rightarrow ln(2^t)=ln((70)/(11)) \\ \Rightarrow t\cdot ln(2)=ln((70)/(11))\Rightarrow t=(ln((70)/(11)))/(ln(2)) \\ \Rightarrow t\cong2.67 \end{gathered}`

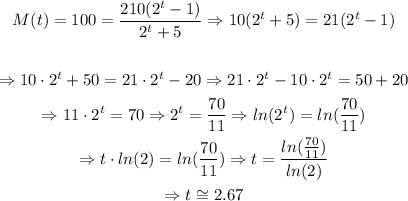
From the solution developed above, we are able to conclude that the solution for the given question is:

t = 2.67