B)
F(t) is continuous for a given value of t if, and only if, the limit for F(t) for t approaching this values by the left and by the right result in the same value. To check it, let us to calculate it, as follows:
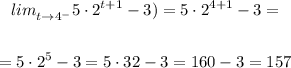

Because the calculation of both side-approaching limits results in different values, we are able to conclude that: The function is not continuous.
C)
To the given equation, we just need to substitute M(t) = 100 and isolate t to find its value, as follows:
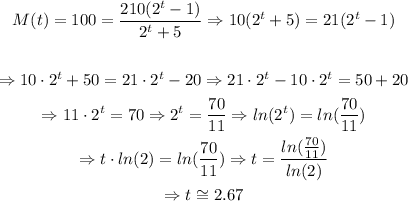
From the solution developed above, we are able to conclude that the solution for the given question is:
t = 2.67