Question

Hi, can you help to Identify the coordinates of the vertex and focus, the equations of the axis ofsymmetry and directrix, and the direction of opening of the parabola with thegiven equation. Then find the length of the latus rectum and graph the parabola. As a result, I don’t need so much explanation.

Answer 1

Given the equation of the parabola:

`x=3(y+1)^2-3`

The general form of the given equation will be as follows:

`4a(x-h)=(y-k)^2`

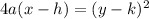
We will write the given equation to be like the general form

`4\cdot(4)/(3)(x+3)=(y+1)^2`

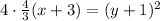
the graph of the parabola will be as follows:

So, the given equation represents a parabola with the following properties:

1) The axis of symmetry is parallel to the x-axis and opens right

2) The coordinates of the vertex = (-3, -1)

3) The equation of the axis of symmetry: y = -1

4) a = 4/3

5) The equation of the directrix: x = h - a ⇒ x = -4 1/3

6) The direction of the opening is right