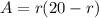Question

Assume the perimeter of a particular sector is 40 cma) Express the measurement of the angle of the sector as a function of the radius of the sector b) express the area of the sector as a function of the radiu

Answer 1

We are asked to determine an equation for the angle of a sector as a function of its radius. To do that let's remember that we have the following relationship:

`s=r\theta`

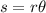
Where "s" is the measurement of the arc of the sector and "r" its radius. Solving for the angle we get:

`\theta=(s)/(r)`

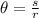
Since we are given the perimeter, we can use the formula for the perimeter of a circular sector:

`P=2r+s`

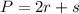
Solving for "s":

`P-2r=s`

Replacing the value of the perimeter:

`40-2r=s`

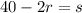
Replacing the value of "s" in the formula for the angle:

`\theta=(40-2r)/(r)`

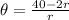
This is the formula for the angle of the sector as a function of the radius.

To find the formula for the area, let's remember that the area of a circular sector is given by the following equation:

`A=(1)/(2)r^2\theta`

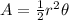
Replacing the value of the angle we get:

`A=(1)/(2)r^2((40-2r)/(r))`

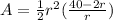
Simplifying:

`A=r(20-r)`