Question

Find the x & y-intercepts for each of the functions. F(x)=2(x-1) (x+2) (x-3)

Answer 1

So we need to find the x and y intercept of these functions:

`\begin{gathered} f(x)=2(x-1) \\ f(x)=x+2 \\ f(x)=x-3 \end{gathered}`

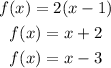
The x and y intercept are the points where the graph of the functions meet the x and y axis respectively. In order to find the x-intercept we must take f(x)=0 and find x. On the other, we can find the y-intercept by taking x=0 and finding the value of f(0). So let's begin with the first one, we take x=0 and we get:

`f(0)=2\cdot(0-1)=2\cdot0-2\cdot1=-2`

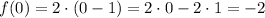
Then we take f(x)=0:

`f(x)=0=2\cdot(x-1)`

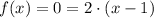
We divide both sides by 2:

`\begin{gathered} (0)/(2)=(2)/(2)\cdot(x-1) \\ 0=x-1 \end{gathered}`

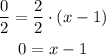
We add 1 at both sides:

`\begin{gathered} 0+1=x-1+1 \\ x=1 \end{gathered}`

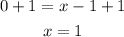
Then for the first function we have:

x-intercept: (1,0)

y-intercept: (0,-2)

Now let's do the same for the second function. If we take x=0 we get:

`\begin{gathered} f(0)=0+2=2 \\ f(0)=2 \end{gathered}`

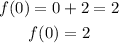
And if we take f(x)=0 we get:

`f(x)=x+2=0`

If we substract 2 from both sides we get:

`\begin{gathered} x+2-2=0-2 \\ x=-2 \end{gathered}`

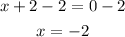
Then for the second function we have:

x-intercept: (-2,0)

y-intercept: (0,2)

Finally if we take x=0 in the third function we get:

`\begin{gathered} f(0)=0-3=-3 \\ f(0)=-3 \end{gathered}`

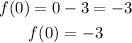
And we take f(x)=0:

`x-3=0`

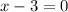
We add 3 to both sides:

`\begin{gathered} x-3+3=0+3 \\ x=3 \end{gathered}`

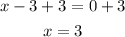
Then for the third function we get:

x-intercept: (3,0)

y-intercept: (0,-3)