Question

Someone help me find m

Answer 1

We know that

`\begin{gathered} m\angle BAC=22 \\ AB\cong BC \\ m\angle CHA=92 \\ CF\parallel HA \end{gathered}`

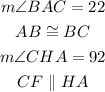
Based on the given information, we can deduct that the triangle ABC is isosceles which implies that the measure of the angle ACB is 22.

Additionally, using the interior angles theorem we can express the following:

`\begin{gathered} 22+22+m\angle ABC=180 \\ m\angle ABC=180-44=136 \end{gathered}`

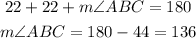
The measure of the angle ABC is 136°.

By supplementary angles, we have.

`\begin{gathered} m\angle ABC+m\angle ABF=180 \\ 136+m\angle ABF=180 \\ m\angle ABF=180-136=44 \end{gathered}`

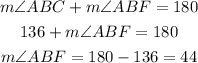
The measure of angle ABF is 44°.

On the other hand, we deduct that angles ABC and BAH are same-side interior angles since they are between parallels at the same side of the transversal AB, they sum 180°.

`m\angle ABC+m\angle BAH=180`

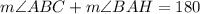
But, the angle BAH is formed by the sum of BAC and CAH.

`\begin{gathered} 136+22+m\angle CAH=180 \\ m\angle CAH=180-158=22 \end{gathered}`

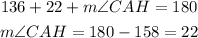
The measure of the angle CAH is 22°.

Using the interior angle theorem we can find the angle ACH.

`\begin{gathered} m\angle ACH+92+22=180 \\ m\angle ACH=180-114=66 \end{gathered}`

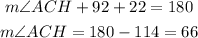
The measure of angle ACH is 66°.

Since CH bisects the angle ACD, we deduct that the measure of the angle HCD is equal to ACH because a bisector divides into two equal parts.

`m\angle HCD=m\angle ACH=66`

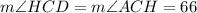
So, the angle ACD would be the sum.

`m\angle ACD=66+66=132`

The measure of angle ACD is 132°.

The measure of angle HCD is 66°.

Then, we solve for angle CDH, we have to once again the interior angle theorem.

`\begin{gathered} m\angle CDH+m\angle CAH+m\angle ACD=180 \\ m\angle CDH+22+132=180 \\ m\angle CDH=180-154=26 \end{gathered}`

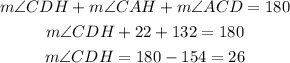
The measure of angle CDH is 26°.

At last, the angle CHD can be found by the supplementary angles theorem which allows us to define the following equation.

`\begin{gathered} 92+m\angle CHD=180 \\ m\angle CHD=180-92=88 \end{gathered}`

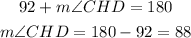
The measure of angle CHD is 88°.