Answer:
Given quadratic function,
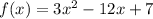
a) To find direction does the parabola open.
First we simplify the given equation in the standard equation of parabola,
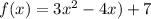
![f\mleft(x\mright)=3\operatorname{\lparen}x^2-4x+4-4)+7]()
![f\mleft(x\mright)=3\operatorname{\lparen}x^2-4x+2^2)-12+7]()
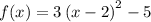
we know that, y=f(x), using this we get,
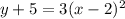
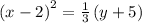
From the standard form of the equation we have that,
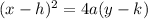
(h,k) is the vertex, and the parabola is open upward.
Hence the parabola is open upward.
b) To find the equation for the axis of symmetry.
The equation of the parabola is,
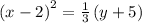
Vertex is (2,-5),
To axis of symmetry passes through the vertex and parallel to y axis since it is open upward.
we get,
Axis of symmetry is,
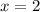
c) To find the coordinates of the vertex,
The equation of the parabola is,
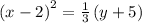
Vertex is (2,-5).