Question

What is the solution set to this equation?108, (2 - 3) + 108, (7 + 3) = 2

Answer 1

We will solve the question using the laws of logarithm

Some of the laws we will use are stated below

`\log_xa+\log_xb=\log_x(a* b)`

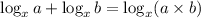
Also ,

`\begin{gathered} \log_xy=z \\ \\ x^z=y \end{gathered}`

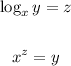
Given ;

`\log_4(x-3)+\log_4(x+3)=2`

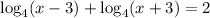
Using same logarithm base ruke , we have

`\log_4(x-3)(x+3)=2`

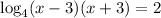
Removing the logarithm , we have

`4^2=(x-3)(x+3)`

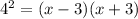
We can now solve the equation obtained as shown below

`\begin{gathered} 16=x^2+3x-3x-9 \\ 16=x^2-9 \\ x^2=16+9 \\ x^2=25 \\ x=\pm√(25) \\ x=\pm5 \end{gathered}`

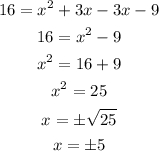
We will ignore x is negative 5 , since we cannot have a negative logarithm

The final answer is x=5

OPTION B