Question

A 97.32 microC charge is fixed at the origin. How much work would be required to place a 14.5 microC charge 11.88 cm from this charge ?

Answer 1

Given:

The charge at the origin is,

`\begin{gathered} Q_1=97.32\text{ }\mu C \\ =97.32*10^(-6)\text{ C} \end{gathered}`

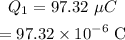
The second charge is,

`\begin{gathered} Q_2=14.5\text{ }\mu C \\ =14.5*10^(-6)\text{ C} \end{gathered}`

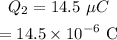
The second charge is at a distance of

`\begin{gathered} r=11.88\text{ cm} \\ =0.1188\text{ m} \end{gathered}`

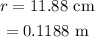
from the origin

To find:

The work to place the second charge

Step-by-step explanation:

The work to place the second charge is,

`\begin{gathered} W=(kQ_1Q_2)/(r) \\ Here,\text{ k=9}*10^9\text{ N.m}^2.C^(-2) \end{gathered}`

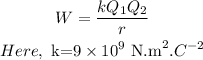
substituting the values we get,

`\begin{gathered} W=(9*10^9*97.32*10^(-6)*14.5*10^(-6))/(0.1188) \\ =106.9\text{ J} \end{gathered}`

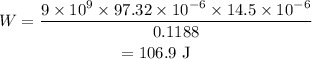
Hence, the required work is 106.9 J.