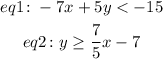
To graph these two equations, we can use their zeroes. Meaning, assume if x = 0, what is y, and if y = 0, what is x.
Let's start with equation no. 1.
if x = 0, then y < -3.
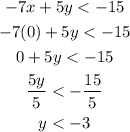
If y = 0, then y > 2.1429
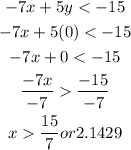
The graph for equation 1 is this:
We are using a dotted line because equation 1 is using the symbol of less than.
Let's graph equation 2.
if x = 0, then y ≥ 7
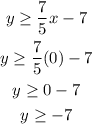
if y = 0, then 5 ≥ x
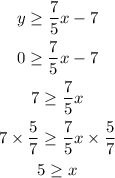
The graph of equation 2 is this:
When the two equations are combined, the graph would look like this:
The solution set of these two equations are the points found in the common area or the points in between the dotted line and the solid line.
Since the question is only asking for a coordinate of one point in the solution set, then we can give this one:
The coordinate (4,2) is one of the solutions of the two equations.
(4, 0) is also a solution.
(4, 1) is also a solution.