Question

A boat heading out to sea starts out at Point A, at horizontal distance of 1189 feet from a lighthouse/the shore. From that point, the boat’s crew measures the angle of elevation to the lighthouse’s beacon-light from that point to be 10°. At some later time, the crew measures the angle of elevation from point B to be 3°. Fine the distance from point A to point B. Round your answer to the nearest tenth of a foot if necessary.

Answer 1

At the point A, the boat is 1189 feet from the lighthouse and the angle of elevation to the lighthouse's beacon-light is 10°.

Therefore, if h is the height of the lighthouse, we have:

`\begin{gathered} \tan10\degree=(h)/(1189) \\ h=1189\cdot\tan10\degree \\ h\approx209.7\text{ feet} \end{gathered}`

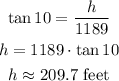
At the point B, the angle of elevation is 3°. Therefore, the distance from the lighthouse d is given by:

`\begin{gathered} \tan3\degree=(h)/(d) \\ d=(h)/(\tan3\degree)\approx4000.4\text{ feet} \\ \end{gathered}`

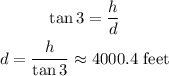
Therefore, the distance between point A and point B is 400.4 - 1189 = 2811.4 feet