The given inequality is,
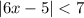
According to absolute rule,
![|y|0 then y>-a and y}Applying absolute rule to the given inequality, [tex]6x-5>-7\text{ and }6x-5<7](https://img.qammunity.org/2023/formulas/mathematics/college/uug5o3i9z1mov3ar998pspxl5qbdxm1u1z.png)
Solving 6x-5>-7,
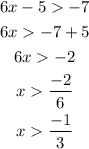
Solving 6x-5<7,
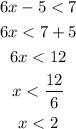
So, the solution is x>-1/3 and x<2.
The solution in interval notation is (-1/3, 2).
Now, the graph of the inequality is,
(Hollow dot in the graph indicates open interval).