Item a):
The Mean Value Theorem states that if a function f is continuous on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists a point c in the interval (a,b) such that f'(c) is equal to the function's average rate of change over [a,b].

Applying this theorem in our problem, we have:
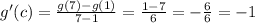
item b):
f(x) is given by the composition of g(x) with itself, therefore, we can calculate the derivative of f(x) by using the chain rule:
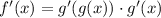
Then, evaluating this expression at x = 1 and x = 7, we have:
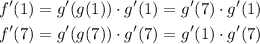
Thus
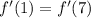
Using the Leibniz rule, we can find the second derivative of f(x):
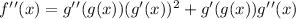
When those two terms are antisymmetric, the second derivative is equal to zero.