we have the equation
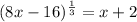
elevated to the cubic on both sides
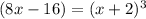
Expand the right side
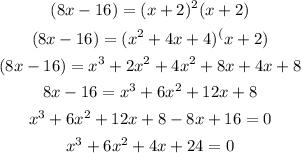
For the cubic equation
For x=-6
the equation is equal to zero
so
x=-6 is a root
Divide the cubic function by the factor (x+6)
x^3+6x^2+4x+24 : (x+6)
x^2+4
-x^3-6x^2
-------------------------
4x+24
-4x-24
--------------
0
therefore
x^3+6x^2+4x+24=(x+6)(x^2+4)
Solve the quadratic equation
x^2+4=0
x^2=-4
x=2i and x=-2i
the solutions are
x=-6
x=2i
x=-2i
Verify in the original equation
For x=-6
![\begin{gathered} \sqrt[3]{(8(-6)-16)}=-6+2 \\ -4=-4\text{ ----> is true} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/teaugsh0o2ls9706ki8cleynvb74sszn6b.png)
The solution is x=-6
x=2i and x=-2i are not solutions for the given equation