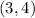Question

Given the following function, what is the vertex?f(x) = -2|x - 3| + 4

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given function

`f(x)=-2|x-3|+4`

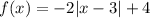
STEP 2: Find the vertex

`\mathrm{Absolute\:value\:function\:vertex\:points\:are\:points\:where\:absolute\:values\:are\:zeros}`

Equate the absolute value to zero to get the vertex

`\begin{gathered} |x-3|=0 \\ x-3=0 \\ x=0+3=3 \end{gathered}`

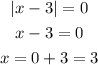
Substitute the value of x to get the y-value

`\begin{gathered} f(x)=-2|x-3|+4 \\ x=3 \\ f(3)=-2(0)+4 \\ f(3)=0+4=4 \end{gathered}`

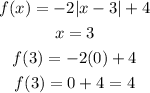
Hence, the vertex of the given function is:

`(3,4)`