The absolute value of cube function F(5)*F(-7) is 42,875
What is absolute value?
The absolute value of a real number is its distance from zero on the number line, regardless of the direction. It is denoted by vertical bars, like |x|, where x is the real number.
Mathematically, if x is greater than or equal to zero, then |x| is equal to x. If x is less than zero, then |x| is equal to the negation of x, making it positive.
Given
F(x) is the function that determines the absolute value of the cube of the input.
F(x) = x³
Absolute function is
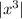
Evaluate F(5)
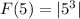
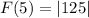
F(5) = 125 absolute value
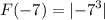
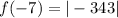
= 343 absolute value
F(5)*F(-7) = 125* 343
= 42,875
The absolute value of cube function F(5)*F(-7) is 42,875