Question

A monochromatic beam of x-rays of wavelength 2.80 x 10^-10 m is scattered by a metal foil. What is the wavelength, in nm, of the scattered x-rays at an angle of 37.37° from the direction of the incident beam?

Answer 1

`\begin{equation*} 81.78\text{ nm} \end{equation*}`

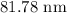
Step-by-step explanation

Wavelength of incident X-rays, λ = 2.80 * 10^-10 m

Scattered angle, θ = 37.37°

To find the wavelength of the scattered x-rays, apply the equation for Compton's effect:

`\lambda^(\prime)-\lambda=(h)/(m_oc)(1-\cos\theta)`

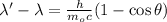
where h = Planck's constant

λ' = wavelength of the scattered x-rays

Substitute the given values into the equation and solve for λ':

`\begin{gathered} \lambda^(\prime)-2.80*10^(-10)=(6.63*10^(-34))/(1.67*10^(-27))(1-\cos37.37) \\ \\ \lambda^(\prime)-2.80*10^(-10)=(6.63*10^(-34))/(1.67*10^(-27))*0.2053 \\ \\ \lambda^(\prime)-2.80*10^(-10)=8.15*10^(-8) \\ \\ \lambda^(\prime)=8.15*10^(-8)+2.80*10^(-10) \\ \\ \lambda^(\prime)=8.178*10^(-8)\text{ m}=81.78\text{ nm} \end{gathered}`

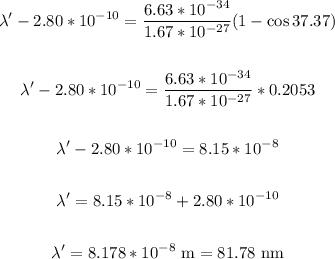
That is the wavelength of the scattered x-rays in nanometers.