Question

Suppose that a is an angle with csc(alpha) = - 11/8 and is not in the third quadrant. Compute the exact value of tan a. You do not have to rationalize the denominator.

Answer 1

we have that

If the cosecant of angle alpha is negative

then

the angle alpha lies on the III or IV quadrant

The problem says that the angle does not lie on the III quadrant

therefore

The angle alpha lies on the IV quadrant

step 1

Find out the value of sine

`\begin{gathered} csc\alpha=(1)/(sin\alpha) \\ \\ sin\alpha=-(8)/(11) \end{gathered}`

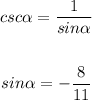
step 2

Find out the value of cosine

`sin^2\alpha+cos^2\alpha=1`

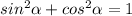
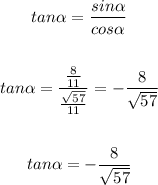
substitute the value of the sine

`\begin{gathered} (-(8)/(11))^2+cos^2\alpha=1 \\ \\ cos^2\alpha=1-(64)/(121) \\ \\ cos^2\alpha=(57)/(121) \\ \\ cos\alpha=(√(57))/(11) \end{gathered}`

step 3

Find out the value of the tangent

`\begin{gathered} tan\alpha=(sin\alpha)/(cos\alpha) \\ \\ tan\alpha=((8)/(11))/((√(57))/(11))=-(8)/(√(57)) \\ \\ tan\alpha=-(8)/(√(57)) \end{gathered}`