Part a)
In the first factorization, Freddy made two mistakes. The first mistake is in step 2 (Which he deleted later) because those two numbers (3 and 4) do not complete the square. The second mistake is more subtle because he factorized correctly but he did not find the correct root.
When you have a factorization in the form of (x-a) (x-b) = 0, the roots (or solutions) can be found if either (x-a) = 0 or (x-b) = 0 :
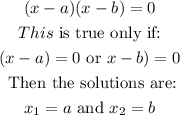
In this first factorization: ( x - (-6) ) ( x - (-2) ) = 0, a = -6 and b = -2.
In the second factorization, he made a mistake assigning the signs of the numbers 10 and 1; and separating the equation into two parts. If you want to factorize correctly a quadratic equation of the form ax^2+bx+c = 0, the first step is:
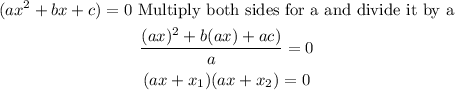
*Notice that the "plus signal" in the first factor comes from the sign of b, i.e. if b is negative then the first factor is negative. However, the second "plus signal" comes from the product of the signs that accompanies b and c.
Part b)
Both answers are wrong because he did not find the roots correctly in the first factorization and he did not factorize correctly the quadratic equation in the second equation.
Part c)
First equation: The solutions are -2 and -6.
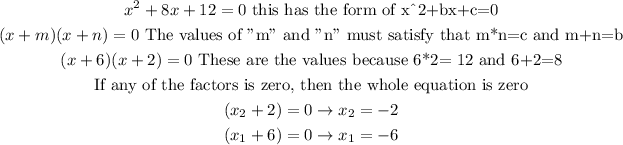
Second equation:

Part d)
To solve equation 1 using the technique of completing the square is just how I solved it before. You first separate them into two factors, then you find the signs of those factors (the first is the sign of b, and the second is the sign of b*c), and finally, you have to find the values of m and n, that satisfy the condition of m+n = b and mn=c.