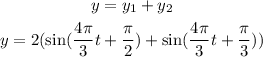The equation for a simple harmonic motion (SHM) is given by:
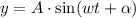
Where A is the amplitude, alpha is the initial phase and the period is given by T = 2π/omega.
So, for A = 2, T = 1.5 and alpha1 = π/2. we have:
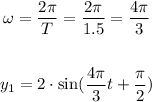
For A = 2, T = 1.5 and alpha = π/3, we have:
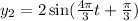
Now, adding both oscillations, we have: