Question

The length of a rectangle is 4 inches longer than twice the width. The perimeter is 50 inches. Find the length and width.

Answer 1

We have a rectangle where the length L is 4 inches longer than twice the width W.

Twice the width is 2W, so we can write the length L as:

`L=2W+4`

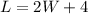
The perimeter is 50 inches.

It is also two times the sum of the length L and the width W, so we can write:

`2(L+W)=50`

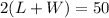
We can replace the length L in the perimeter equation and then solve for W as:

`\begin{gathered} 2(L+W)=50 \\ 2\lbrack(2W+4)+W\rbrack=50 \\ 2W+4+W=(50)/(2) \\ 3W+4=25 \\ 3W=25-4 \\ 3W=21 \\ W=(21)/(3) \\ W=7 \end{gathered}`

Knowing the width, we can calculate the length L as:

`\begin{gathered} L=2W+4 \\ L=2(7)+4 \\ L=14+4 \\ L-18 \end{gathered}`

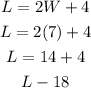
Answer: the rectangle is 18 inches long and 7 inches wide.